Peter Kliche - Mittelpunktswinkel

Mittelpunktswinkel - Umfangswinkel

siehe auch Wikibooksi Wikipedia (Die freie Enzyklopädie)

Nachweis, dass der Mittelpunktswinkel $ϕ$ doppelt so groß wie der Umfangswinkel $γ$ ist:

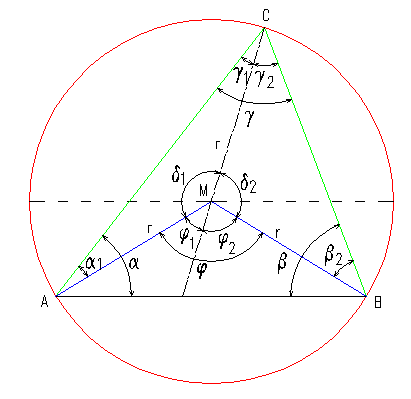
Das Dreieck AMC ist ein gleichschenkliges Dreieck (AM=MC=r). Die anliegenden Winkel sind deshalb gleich groß:

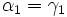$\alpha _1 = \gamma _1 \,$

Winkelsumme im Dreieck:

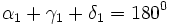$\alpha _1 + \gamma _1 + \delta _1 = 180^0 \,$

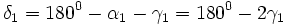$\delta _1 = 180^0 - \alpha _1 - \gamma _1 = 180^0 - 2\gamma _1 \,$

Winkel der Geraden 180°:

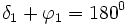$\delta _1 + \varphi _1 = 180^0 \,$

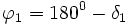$\varphi _1 = 180^0 - \delta _1 \,$

eingesetzt ergibt sich:

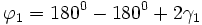$\varphi _1 = 180^0 - 180^0 + 2\gamma _1 \,$

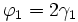$\varphi _1 = 2\gamma _1 \,$

Für das Dreieck BMC gilt dasselbe, so dass analog gilt:

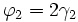$\varphi _2 = 2\gamma _2 \,$

und damit:

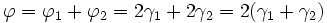$\varphi = \varphi _1 + \varphi _2 = 2\gamma _1 + 2\gamma _2 = 2(\gamma _1 + \gamma _2 )\,$

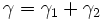$\gamma = \gamma _1 + \gamma _2 \,$

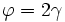$\varphi = 2\gamma \,$

Da der Punkt C beliebig auf dem Kreisbogen verschoben werden kann, gilt dieser Nachweis für alle Umfangswinkel. Damit ist auch der Beweis erbracht, dass alle Umfangswinkel über derselben Sehne AB gleich sind.

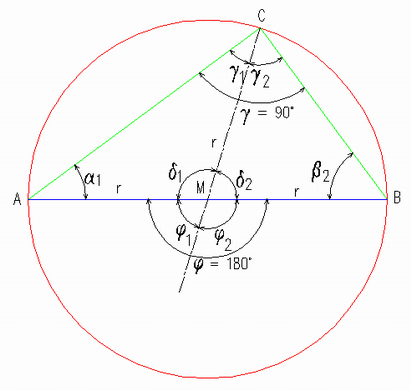
Weiter lässt sich mit diesem Nachweis auch der Sonderfall Satz des Thales nachweisen: Die Sehne AB liegt dann genau auf dem Durchmesser und damit ist:

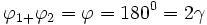
$\varphi _{1 + } \varphi _2 = \varphi = 180^0 = 2\gamma \,$

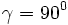$\gamma = 90^0 \,$

Sonderfall Thaleskreis