PETER KLICHE
| Regelmäßige Vielecke: Fünfeck |
||||
| siehe auch Wikibooks Wikipedia(Die freie Enzyklopädie) |  |
|||
| Regelmäßiges Fünfeck (Pentagon) | ||||
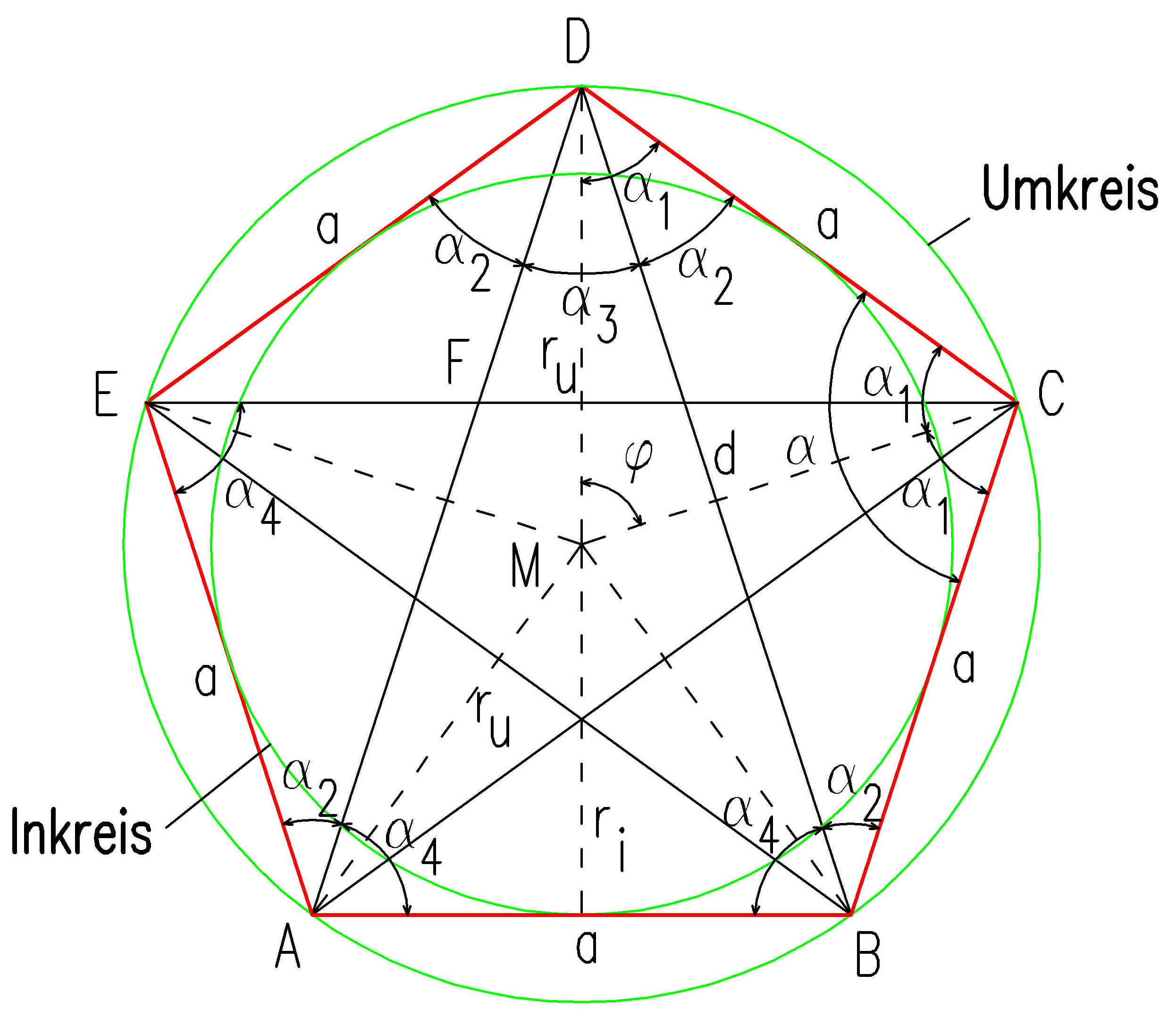 |
||||
| Winkel im regelmäßigen Fünfeck (Pentagon) | ||||
| Im Mittelpunkt M | ||||
| (1) | 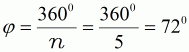 |
Mittelpunkswinkel | ||
| Winkelsumme im gleichschenkligen Dreieck CDM | ||||
| (2) | ||||
| (2a) | 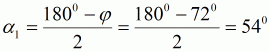 |
|||
| Innenwinkel im Fünfeck | ||||
| (2b) | Innenwinkel Fünfeck | |||
| Winkelsumme im gleichschenkligen Dreieck BCD | ||||
| (2c) | ||||
| (2d) | 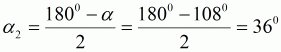 |
|||
| im Winkel D | ||||
| (3a) | ||||
| (3b) | ||||
| im gleichschenkligen Dreieck ADB | ||||
| (4) | ||||
| (4a) | 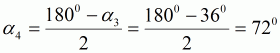 |
|||
| Längen im regelmäßigen Fünfeck (Pentagon) | ||||
| Die Dreiecke ABD und FEA sind ähnlich, weil die Winkel in Punkt A und D | ||||
| und die Winkel in Punkt E und A | ||||
| gleich sind | ||||
| (5) | ||||
| (6) | ||||
| (6a) | ||||
| (6b) | ||||
| (6c) | ||||
| (6d) | ||||
| Diagonale | ||||
| (6) bis (6d) in (5) eingesetzt | ||||
| (7) | 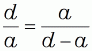 |
|||
| (7a) | ||||
| (7b) | ||||
| Lösung der quadratischen Gleichung | ||||
| (8) | 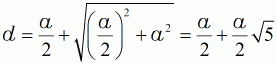 |
|||
| (8a) | 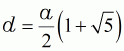 |
Diagonale | ||
| Inkreisradius | ||||
| (8a) quadriert | ||||
| (9) | 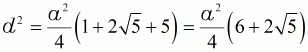 |
|||
| (9a) | 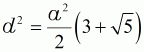 |
|||
| nach Pythagoras | ||||
| (10) | 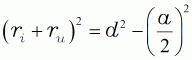 |
|||
| (9a) eingesetzt | ||||
| (10a) | 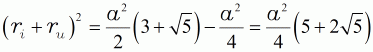 |
|||
| daraus die Wurzel | ||||
| (11) | 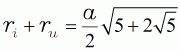 |
|||
| ebenfalls nach Pythagoras | ||||
| (12) | 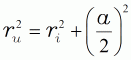 |
|||
| (12a) | 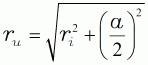 |
|||
| (12a) in (11) eingesetzt | ||||
| (13) | 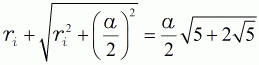 |
|||
| (13a) | 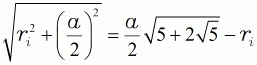 |
|||
| quadriert | ||||
| (13b) | 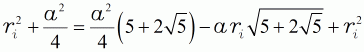 |
|||
| (13c) | 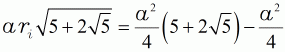 |
|||
| (14) | 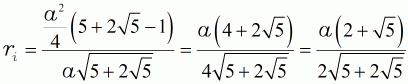 |
|||
| erweitert | ||||
| (14a) | 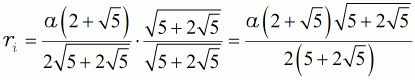 |
|||
| erweiter | ||||
| (14b) | 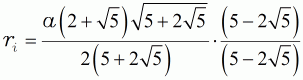 |
|||
| ausgerechnet | ||||
| (14c) | 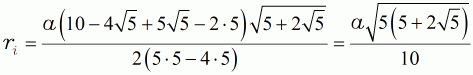 |
|||
| (14d) | 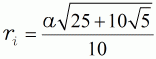 |
Inkreisradius | ||
| Umkreisradius | ||||
| (14d) in (12a) eingesetzt | ||||
| (15) | 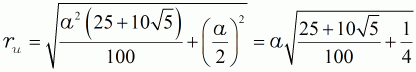 |
|||
| (15a) | 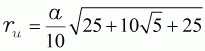 |
|||
| (15b) | 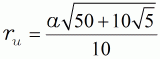 |
Umkreisradius | ||
| Höhe | ||||
| (16) | ||||
| Formel (11) eingesetzt | ||||
| (16a) | 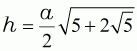 |
Höhe | ||
| Fläche | ||||
| (17) | 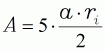 |
|||
| (14d) in (17) eingesetzt | ||||
| (17a) | 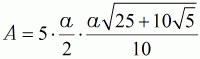 |
|||
| (17b) | 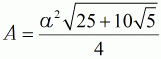 |
Fläche | ||
| <Zurück | ||
| Homepage | Impressum | Kontakt | Über mich | Datenschutz |